Límite de una sucesión de conjuntos

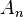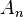En teoría de conjuntos también se utiliza el concepto de límite, que se puede calcular sobre una sucesión de conjuntos. Para ello, los conjuntos deben de cumplir una serie de condiciones, como puede ser la monotonía (creciente o decreciente). De manera más general, y utilizando la definición de límite superior y límite inferior para una sucesión de conjuntos cualquiera , se dice que el límite de esta sucesión existe si el límite superior y límite inferior existen y son iguales,

Estos conceptos son muy útiles en disciplinas de las matemáticas como la teoría de la medida, especialmente en espacios de probabilidad.