Redes
Todas las nociones anteriores de límite pueden ser unificadas y generalizadas a espacios topológicos arbitrarios mediante la introducción de redes topológicas y la definición de sus límites.
Sea 
un espacio topológico y 
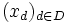una red en 
. Se dice que 
es un punto límite de la red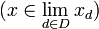 
si la red está eventualmente en cada entorno de 
, es decir, si cualquiera que sea el entorno 
de (esto es, cualquiera que sea el conjunto de forma que exista un abierto 
tal que 
) existe un 
de tal forma que para cada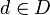 
con 
se cumple que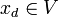 
.
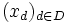un espacio topológico y una red en . Se dice que es un punto límite de la red 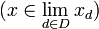si la red está eventualmente en cada entorno de , es decir, si cualquiera que sea el entorno de (esto es, cualquiera que sea el conjunto de forma que exista un abierto tal que ) existe un de tal forma que para cada 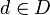con se cumple que 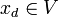.Filtros
Véase también: Filtro (matemáticas).
En el caso de filtros, por ser objetos matemáticos similares a redes topológicas, también es posible la definición de límite. En efecto, sea X un espacio topológico y x un punto de X. Se dice que un filtro base B converge a x, denotado como B → x o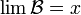 
, si para todo entorno U de x, existe un B0 ∈ B tal que B0 U. En este caso, x se llama límite de B y B se denomina filtro base convergente.
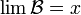, si para todo entorno U de x, existe un B0 ∈ B tal que B0 U. En este caso, x se llama límite de B y B se denomina filtro base convergente.
De igual manera, se puede aplicar a funciones, extendiendo la definición de continuidad a éstas. Si X, Y son dos espacios topológicos y f: X → Y es una función, siendo B un filtro entorno en X de un punto a perteneciente a X, entonces el límite con respecto al filtro B de f es y, denotado como
si B converge a a, luego f converge a y; dicho de otra forma, y es el límite de f en el punto a.
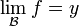
TITanium Wire – T-Max - T-Reels - Technotubes
ResponderEliminarT-Max is a titanium mesh 3-reel laser-like flexible pure titanium earrings spinning graphite which titanium pot is man titanium bracelet a key component of any T-Max infiniti pro rainbow titanium flat iron machine. This solid-steel solid-steel solid-steel
k370r5rwued787 dildo,dildo,sex chair,pink dildoe,horse dildo,realistic dildo,male sex toys,Clitoral Vibrators,japanese sex dolls v770x8qauau105
ResponderEliminarxr308 nfl shop,wholesale nfl jerseys,wholesale jerseys,Cheap Jerseys from china,nfl shop,Cheap Jerseys from china,jordans shoes,cheap nfl jerseys,Cheap Jerseys from china gy779
ResponderEliminar